Research

Adaptive Annealing for Robust Averaging
	Graduated Non-Convexity (GNC) or Annealing is a popular technique in robust cost minimization for its ability to converge to good local minima irrespective of initialization. However, the conventional use of a fixed annealing scheme in GNC often leads to a poor efficiency vs accuracy tradeoff. To address it, previous approaches introduced adaptive annealing but lacked scalability for large optimization problems. \textit{Averaging} of pairwise relative observations is one such class of problems, defined on a graph, wherein a large number of variables (nodes) are estimated given the pairwise observations (edges). In this paper, we present a novel adaptive GNC framework tailored for averaging problems in computer vision, operating on vector spaces. Leveraging insights from graph Laplacian matrices inherent in such problems, our approach imparts scalability to the principled GNC framework. Our method demonstrates superior accuracy in vector averaging and translation averaging, while maintaining efficiency comparable to baselines.
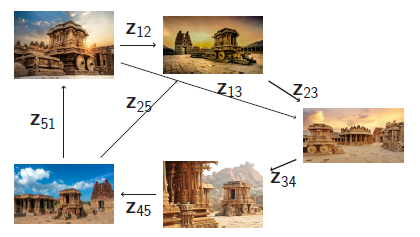
Leveraging Camera Triplets for Efficient and Accurate Structure-from-Motion
In Structure-from-Motion (SfM), the underlying viewgraphs of unordered image collections generally have a highly redundant set of edges that can be sparsified for efficiency without significant loss of reconstruction quality. Often, there are also false edges due to incorrect image retrieval and repeated structures (symmetries) that give rise to ghosting and superimposed reconstruction artifacts. We present a unified method to simultaneously sparsify the viewgraph and remove false edges. We propose a scoring mechanism based on camera triplets that identifies edge redundancy as well as false edges. Our edge selection is formulated as an optimization problem which can be provably solved using a simple thresholding scheme. This results in a highly efficient algorithm which can be incorporated as a pre-processing step into any SfM pipeline, making it practically usable. We demonstrate the utility of our method on generic and ambiguous datasets that cover the range of small, medium and large-scale datasets, all with different statistical properties. Sparsification of generic datasets using our method significantly reduces reconstruction time while maintaining the accuracy of the reconstructions as well as removing ghosting artifacts. For ambiguous datasets, our method removes false edges, thereby avoiding incorrect superimposed reconstructions.
Fusing Directions and Displacements in Translation Averaging
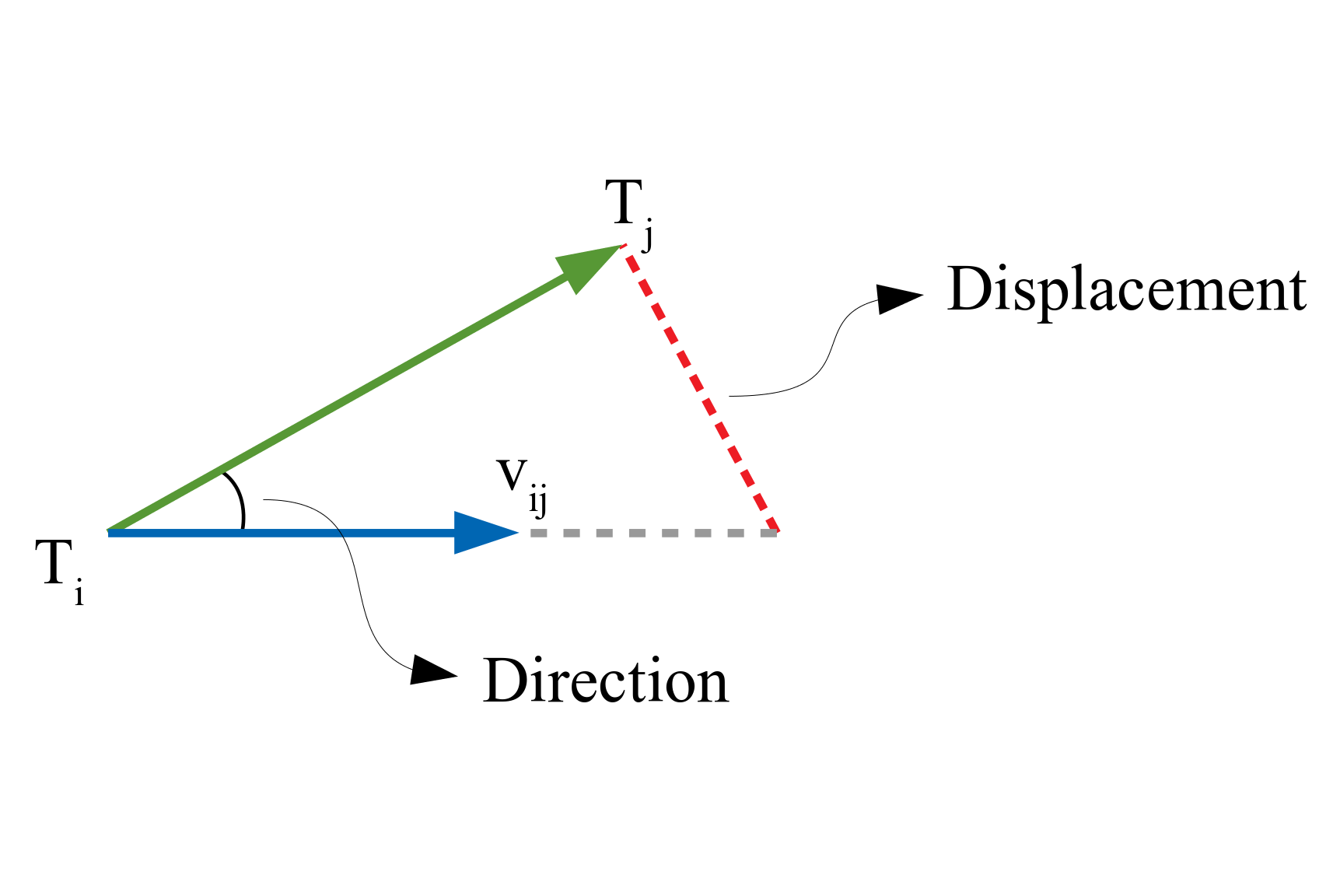	Translation averaging solves for 3D camera translations given many pairwise relative translation directions. The mismatch between inputs (directions) and output estimates (absolute translations) makes translation averaging a challenging problem, which is often addressed by comparing either directions or displacements using relaxed cost functions that are relatively easy to optimize. However, the distinctly different nature of the cost functions leads to varied behaviour under different baselines and noise conditions. In this paper, we argue that translation averaging can benefit from a fusion of the two approaches. Specifically, we recursively fuse the individual updates suggested by direction and displacement-based methods using their uncertainties. The uncertainty of each estimate is modelled by the inverse of the Hessian of the corresponding optimization problem. As a result, our method utilizes the advantages of both methods in a principled manner. The superiority of our translation averaging scheme is demonstrated via the improved accuracies of camera translations on benchmark datasets compared to the state-of-the-art methods.
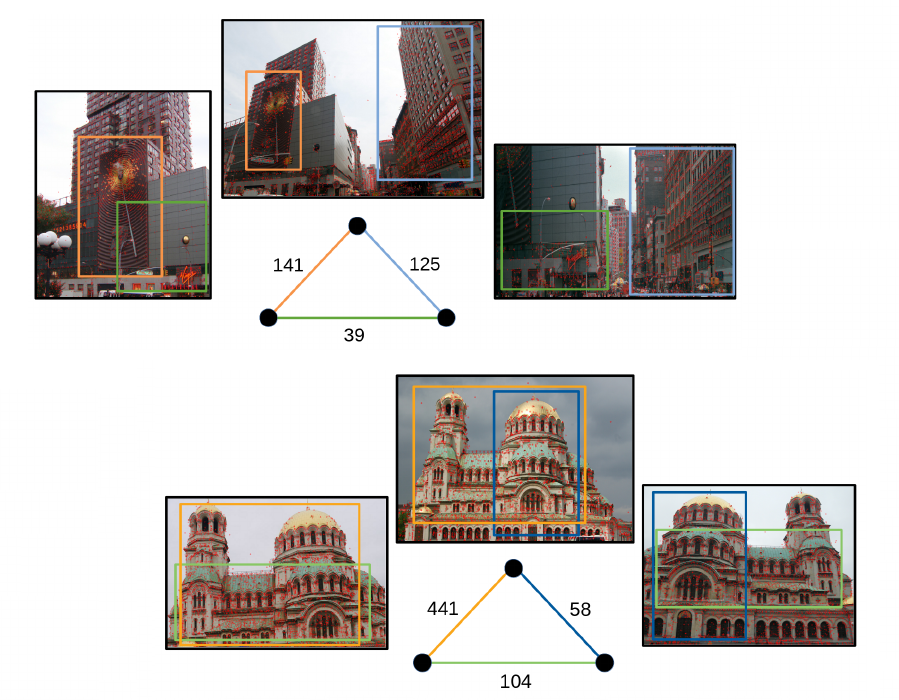
Sensitivity in Translation Averaging
In 3D computer vision, translation averaging solves for absolute translations given a set of pairwise relative translation directions. While there has been much work on robustness to outliers and studies on the uniqueness of the solution, this paper deals with a distinctly different problem of sensitivity in translation averaging under uncertainty. We first analyze sensitivity in estimating scales corresponding to relative directions under small perturbations of the relative directions. Then, we formally define the conditioning of the translation averaging problem, which assesses the reliability of estimated translations based solely on the input directions. We give a sufficient criterion to ensure that the problem is well-conditioned. Subsequently, we provide an efficient algorithm to identify and remove combinations of directions which make the problem ill-conditioned while ensuring uniqueness of the solution. We demonstrate the utility of such analysis in global structure-from-motion pipelines for obtaining 3D reconstructions, which reveals the benefits of filtering the ill-conditioned set of directions in translation averaging in terms of reduced translation errors, a higher number of 3D points triangulated and faster convergence of bundle adjustment.
Adaptive Annealing for Robust Geometric Estimation
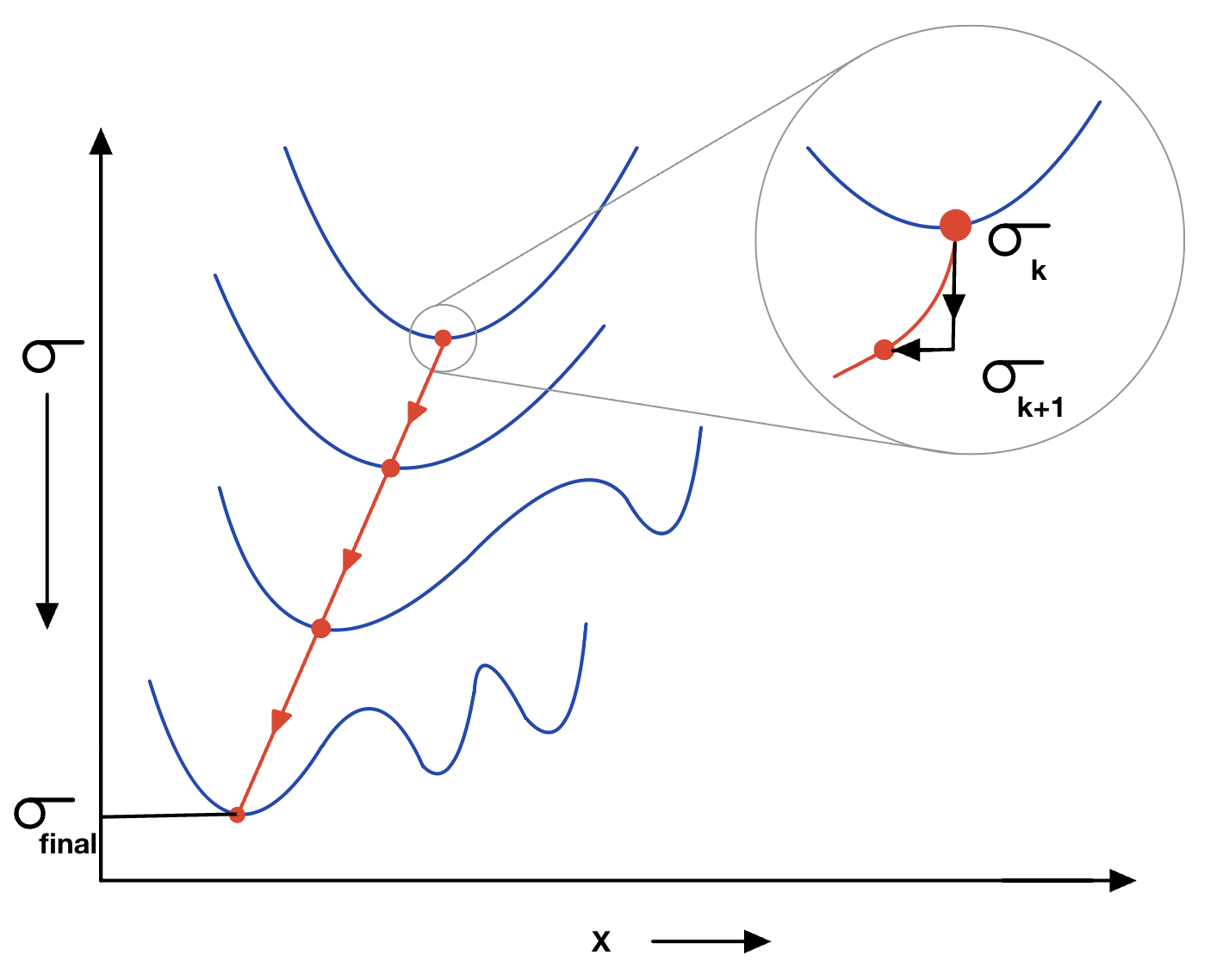	Geometric estimation problems in vision are often solved via minimization of statistical loss functions which account for the presence of outliers in the observations. The corresponding energy landscape often has many local minima. Many approaches attempt to avoid local minima by annealing the scale parameter of loss functions using methods such as graduated non-convexity (GNC). However, little attention has been paid to the annealing schedule, which is often carried out in a fixed manner, resulting in a poor speed-accuracy trade-off and unreliable convergence to the global minimum. In this paper, we propose a principled approach for adaptively annealing the scale for GNC by tracking the positive-definiteness (i.e. local convexity) of the Hessian of the cost function. We illustrate our approach using the classic problem of registering 3D correspondences in the presence of noise and outliers. We also develop approximations to the Hessian that significantly speeds up our method. The effectiveness of our approach is validated by comparing its performance with state-of-the-art 3D registration approaches on a number of synthetic and real datasets. Our approach is accurate and efficient and converges to the global solution more reliably than the state-of-the-art methods.
Correspondence Reweighted Translation Averaging
The problem of estimating camera translations is addressed in this work. Instead of just using the relative translation directions obtained from epipolar geometry, point correspondences are used in the formulation. Each point correspondence is weighted based on global consistency which is used to estimate relative translations. These relative translations are then taken as input to a translation averaging scheme. This is performed in an alternating manner. The translation solutions improve the reconstructions on unordered image data collections with global structure-from-motion pipeline.
Efficient and Robust Large-Scale Rotation Averaging
	The problem of robust and efficient averaging of relative 3D rotations is addressed in this work. Apart from having an interesting geometric structure, robust rotation averaging addresses the need for a good initialization for large-scale optimization used in structure-from-motion pipelines. Such pipelines often use unstructured image datasets harvested from the internet thereby requiring an initialization method that is robust to outliers. This approach works on the Lie group structure of 3D rotations and solves the problem of large-scale robust rotation averaging in two ways. Firstly, modern L1 optimizer is used to carry out robust averaging of relative rotations that is efficient, scalable and robust to outliers. In addition, a twostep method has also been developed that uses the L1 solution as an initialization for an iteratively reweighted least squares (IRLS) approach. These methods achieve excellent results on large-scale, real world datasets and significantly outperform existing methods, i.e. the state-of-the-art discrete-continuous optimization method as well as the Weiszfeld method. The efficacy of this method is demonstrated on two large-scale real world dataset.
Photometric Refinement of Depth Maps for Multi-albedo Objects
In this work, we propose a novel uncalibrated photometric method for refining depth maps of multi-albedo objects obtained from consumer depth cameras like Kinect. Existing uncalibrated photometric methods either assume that the object has constant albedo or rely on segmenting images into constant albedo regions. Our method does not require the constant albedo assumption and we believe it is the first work of its kind to handle objects with arbitrarily varying albedo under uncalibrated illumination.
High Quality Photometric Reconstruction using a Depth Camera
	In this work, we develop a depth-guided photometric 3D reconstruction method that works solely with a depth camera like the Kinect. Existing methods that fuse depth with normal estimates use an external RGB camera to obtain photometric information and treat the depth camera as a black box that provides a low quality depth estimate. Our contribution to such methods are two fold. Firstly, instead of using an extra RGB camera, we use the infra-red (IR) camera of the depth camera system itself to directly obtain high resolution photometric information. We believe that ours is the first method to use an IR depth camera system in this manner. Secondly, photometric methods applied to complex objects result in numerous holes in the reconstructed surface due to shadows and self-occlusions. To mitigate this problem, we develop a simple and effective multiview reconstruction approach that fuses depth and normal information from multiple viewpoints to build a complete, consistent and accurate 3D surface representation.
A Pipeline for Building 3D Models using Depth Cameras
In this work we describe a system for building geometrically consistent 3D models using structured-light depth cameras. While the commercial availability of such devices, i.e. Kinect, has made obtaining depth images easy, the data tends to be corrupted with high levels of noise. In order to work with such noise levels, our approach decouples the problem of scan alignment from that of merging the aligned scans. The alignment problem is solved by using two methods tailored to handle the effects of depth image noise and erroneous alignment estimation. The noisy depth images are smoothed by means of an adaptive bilateral filter that explicitly accounts for the sensitivity of the depth estimation by the scanner. Our robust method overcomes failures due to individual pairwise ICP errors and gives alignments that are accurate and consistent. Finally, the aligned scans are merged using a standard procedure based on the signed distance function representation to build a full 3D model of the object of interest. We demonstrate the performance of our system by building complete 3D models of objects of different physical sizes, ranging from cast-metal busts to a complete model of a small room as well as that of a complex scale model of an aircraft.
Efficient Higher Order Clustering on the Grassmann Manifold
	The higher-order clustering problem arises when data is drawn from multiple subspaces or when observations fit a higher-order parametric model. Most solutions to this problem either decompose higher-order similarity measures for use in spectral clustering or explicitly use low-rank matrix representations. In this project we present our approach of Sparse Grassmann Clustering (SGC) that combines attributes of both categories. While we decompose the higherorder similarity tensor, we cluster data by directly finding a low dimensional representation without explicitly building a similarity matrix. By exploiting recent advances in online estimation on the Grassmann manifold (GROUSE) we develop an efficient and accurate algorithm that works with individual columns of similarities or partial observations thereof. Since it avoids the storage and decomposition of large similarity matrices, our method is efficient, scalable and has low memory requirements even for large-scale data.
Symmetric Smoothing Filters from Global Consistency Constraint
Many patch-based image denoising methods can be viewed as data-dependent smoothing filters that carry out a weighted averaging of similar pixels. It has recently been argued that these averaging filters can be improved by taking their doubly stochastic approximation thereby making them symmetric and stable smoothing operators. In this work, we introduce a simple principle of consistency that argues that the relative similarities between pixels as imputed by the averaging matrix should be preserved in the filtered output. The resultant consistency filter has the theoretically desirable properties of being symmetric, stable and is a generalized doubly stochastic matrix. In addition, we can also interpret our consistency filter as a specific form of Laplacian regularization. Thus, our approach unifies two strands of image denoising methods, i.e. symmetric smoothing filters and spectral graph theory. Our consistency filter provides high quality image denoising and significantly outperforms the doubly stochastic version.