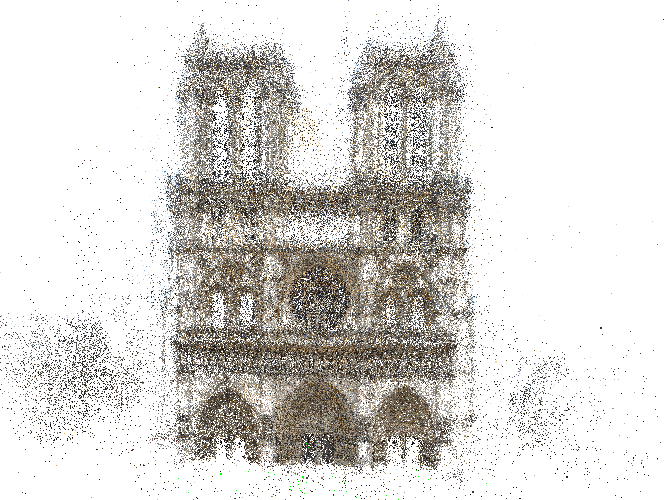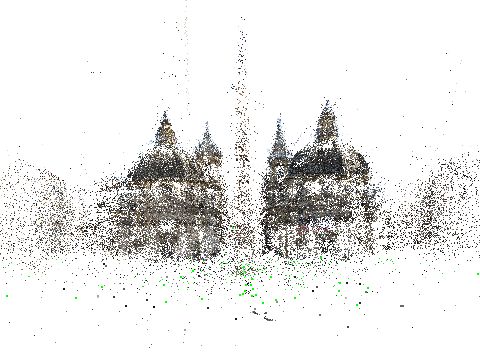Lalit Manam, Venu Madhav Govindu
[Paper] [Supp] [Poster] [Video] [Code] (Updated July 16, 2022)
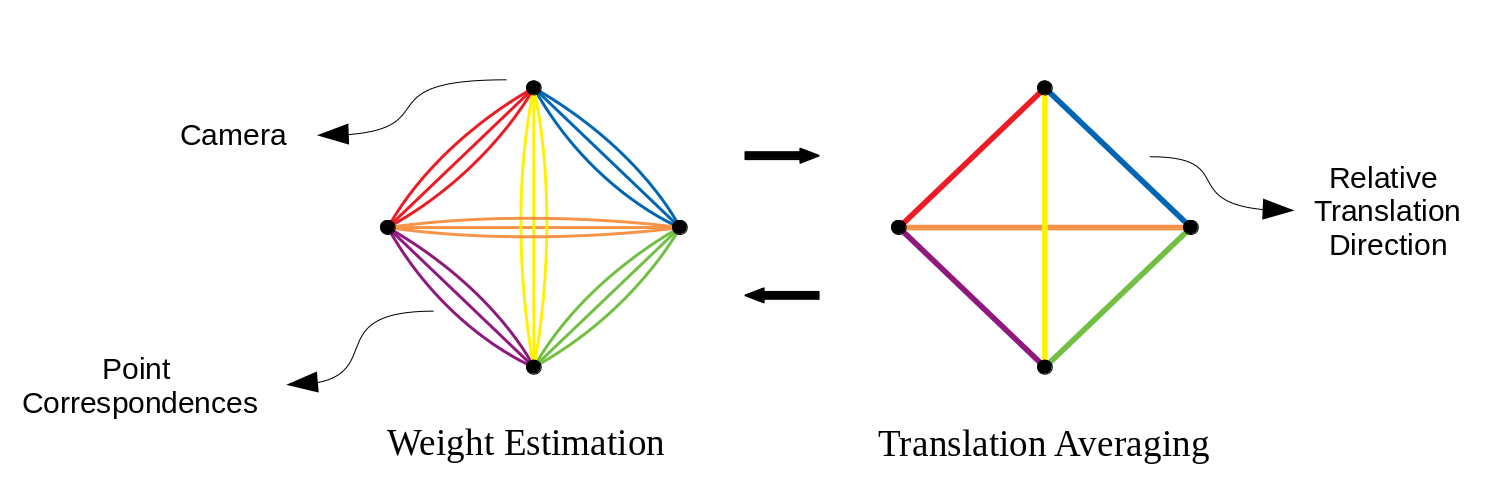
Translation averaging methods use the consistency of input translation directions to solve for camera translations. However, translation directions obtained using epipolar geometry are error-prone. This paper argues that the improved accuracy of translation averaging should be leveraged to mitigate the errors in the input translation direction estimates. To this end, we introduce weights for individual correspondences which are iteratively refined to yield improved translation directions. In turn, these refined translation directions are averaged to obtain camera translations. This results in an alternating approach to translation averaging. The modularity of our framework allows us to use existing translation averaging methods and improve their results. The efficacy of the scheme is demonstrated by comparing performance with state-of-the-art methods on a number of real-world datasets. We also show that our approach yields reasonably good 3D reconstructions with straightforward triangulation, i.e. without any bundle adjustment iterations.
|
|
|---|
Notations
- Underlying viewgraph: \( \mathcal{G}=\left(\mathcal{V},\mathcal{E}\right) \).
- Global rotation and translation: \(\mathbf{R}_{i} \in \mathbb{SO}(3), \mathbf{T}_{i} \in \mathbb{R}^{3}, \forall i \in \mathcal{V} \).
- Relative rotation and translation direction:
\(
\mathbf{R}_{ij}= \mathbf{R}_j \mathbf{R}_i^{-1}, \mathbf{t}_{ij}= \frac{\mathbf{R}_j(\mathbf{T}_i-\mathbf{T}_j)}{\|\mathbf{R}_j(\mathbf{T}_i-\mathbf{T}_j)\|_2}, \forall \left(i,j\right) \in \mathcal{E}
\).
- Relative translation direction in global reference frame:
\(
\mathbf{v}_{ij}=-\mathbf{R}_j^{-1} \mathbf{t}_{ij}= \frac{\mathbf{T}_j-\mathbf{T}_i}{\|\mathbf{T}_j-\mathbf{T}_i\|_2}, \forall \left(i,j\right) \in \mathcal{E}
\).
- \( k^{th} \) correspondence in the edge \( \left(i,j\right) \) : \(\mathbf{p}_i^k\) and \(\mathbf{q}_j^{k}\).
- \(\lambda_{ij}\) and \(\gamma_{ij}\): Non-negative variables that are ideally equal to baseline and inverse baseline for the edge \((i,j)\) respectively.
Method
The epipolar geometry relates the point correspondences using the relative motion as:
\begin{align}
&\left(\mathbf{q}_j^{k}\right)^T \left( \mathbf{t}_{ij} \times \mathbf{R}_{ij} \mathbf{p}_i^k \right) =0 \\
\Rightarrow & \left(\mathbf{m}_{ij}^{k}\right)^T \mathbf{v}_{ij} =0 \text{ (with known rotations)}
\end{align}
We formulate our framework using the epipolar relation as:
\begin{equation}
\min_{\mathbb{T}} \sum_{(i,j)\in \mathcal{E}} {\|\mathbf{W}_{ij} \mathbf{M}_{ij} \mathbf{v}_{ij}(\mathbb{T}) \|}_2^{2} \label{Eqn:JointCost}
\end{equation}
- \(\mathbf{v}_{ij}\): dependent on global translations \(\mathbb{T}\).
- \(\mathbf{W}_{ij}\): diagonal matrix of weights \(\mathbf{w}_{ij}^k\) based on global consistency of translation directions.
Given an initial set of translations \(\mathbb{T}\), weights \(\mathbf{w}_{ij}^k\) are updated. Then \(\mathbf{v}_{ij}\)'s are estimated with the weighted correspondences.
Using \(\mathbf{v}_{ij}\)'s, translation averaging is solved. This is repeated until convergence.
Two representative translation averaging schemes are used:
-
Revised LUD or RLUD (compares displacement vectors):
\begin{align*}
\min_{\mathbf{T}_{i, i \in \mathcal{V}}, \lambda_{ij, (i,j) \in \mathcal{E}} } & \| \mathbf{T}_j - \mathbf{T}_i - \lambda_{ij} \mathbf{v}_{ij} \|_2 \label{eqn:RLUDFormulation} \\
\text{s.t. } \sum_{i \in \mathcal{V}} \mathbf{T}_i =\mathbf{0}, \sum_{(i,j) \in \mathcal{E}} & \left\langle \mathbf{T}_j - \mathbf{T}_i, \mathbf{v}_{ij} \right\rangle =1,
\lambda_{ij} \ge 0, \text{ } \forall (i,j) \in \mathcal{E}
\end{align*}
-
BATA (compares directions):
\begin{align*}
\min_{\mathbf{T}_{i, i \in \mathcal{V}}, \gamma_{ij, (i,j) \in \mathcal{E}} } & \rho \left( \| \left(\mathbf{T}_j - \mathbf{T}_i\right) \gamma_{ij} - \mathbf{v}_{ij} \|_2 \right) \label{eqn:BATAFormulation} \\
\text{s.t. } \sum_{i \in \mathcal{V}} \mathbf{T}_i =\mathbf{0}, \sum_{(i,j) \in \mathcal{E}} & \left\langle \mathbf{T}_j - \mathbf{T}_i, \mathbf{v}_{ij} \right\rangle =1,
\gamma_{ij} \ge 0, \text{ } \forall (i,j) \in \mathcal{E}
\end{align*}
These methods are referred as CReTA-RLUD and CReTA-BATA when used within the CReTA framework.
Results
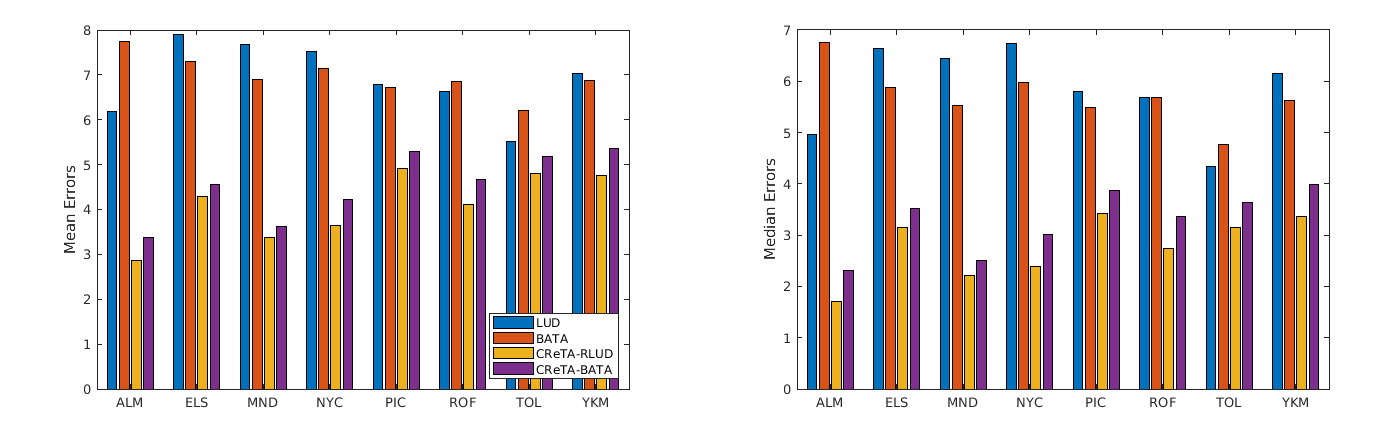
Figure 1. Reprojection errors (in pixels) after triangulation on 1DSfM datasets using the translation solution obtained from dataset provided initialization
Figure 2. Reconstructions obtained with triangulation using our CReTA-RLUD translation estimate (first row) compared to bundle adjustment (second row)
Publication
-
Correspondence Reweighted Translation Averaging (Lalit Manam and Venu Madhav Govindu), European Conference on Computer Vision, 2022. [bibtex]