Lalit Manam, Venu Madhav Govindu
[Paper] [Poster] [Video] [Code] (Updated Dec 1, 2023)
In 3D computer vision, translation averaging solves for absolute translations given a set of pairwise relative translation directions. While there has been much work on robustness to outliers and studies on the uniqueness of the solution, this paper deals with a distinctly different problem of sensitivity in translation averaging under uncertainty. We first analyze sensitivity in estimating scales corresponding to relative directions under small perturbations of the relative directions. Then, we formally define the conditioning of the translation averaging problem, which assesses the reliability of estimated translations based solely on the input directions. We give a sufficient criterion to ensure that the problem is well-conditioned. Subsequently, we provide an efficient algorithm to identify and remove combinations of directions which make the problem ill-conditioned while ensuring uniqueness of the solution. We demonstrate the utility of such analysis in global structure-from-motion pipelines for obtaining 3D reconstructions, which reveals the benefits of filtering the ill-conditioned set of directions in translation averaging in terms of reduced translation errors, a higher number of 3D points triangulated and faster convergence of bundle adjustment.
|
|
|---|
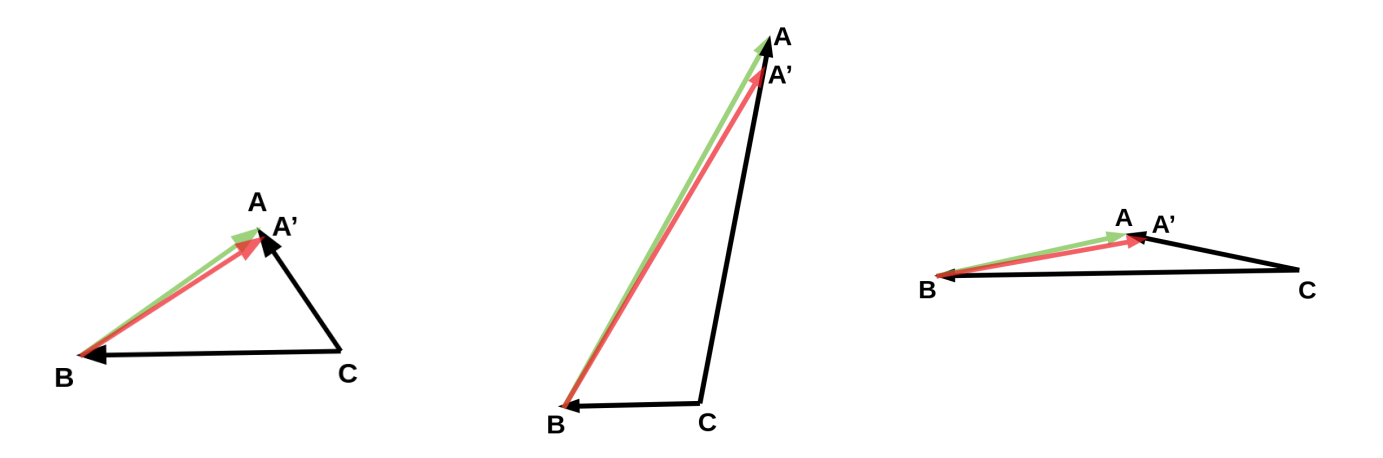
Conditioning in Triangles
The top figure shows three directions in different conditions. The left subfigure shows a configuration when the angles between the directions are sufficiently large. In this case, small perturbations (green to red) to the directions lead to small changes in the absolute translations (A to A') making it well-conditioned. In the middle and right subfigures, atleast one angle between the directions are close to zero. Small perturbations in such cases lead to large changes in the absolute translations making them ill-conditioned.
Theoretical Contributions
- Understanding sensitivity in estimating scales from directions for the smallest solvable problem i.e. a triangle.
- Defining skewness of a triangle based on conditioning of a specific matrix named angle matrix.
- Extending the angle matrix to define conditioning of the translation averaging for networks consisting only of triplets.
- Ensuring uniqueness of the solution (parallel rigidity) based on the graph structure.
Analysis of Real Data

The above figure shows the reconstruction of Alamo dataset. Skewed triangles exist in real datasets as seen in blue and green. We remove such skewed triangles to obtain reliable absolute translations (from input directions).
|  |
 |
 |
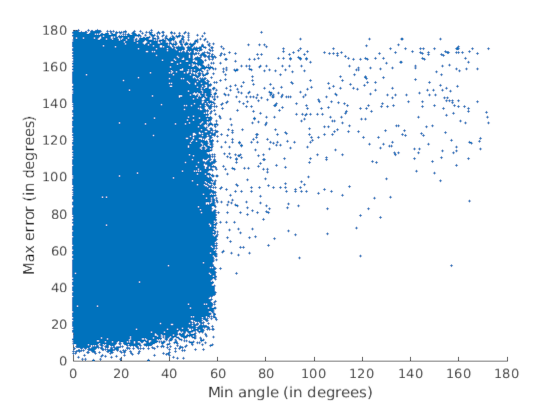
| Piccadilly |
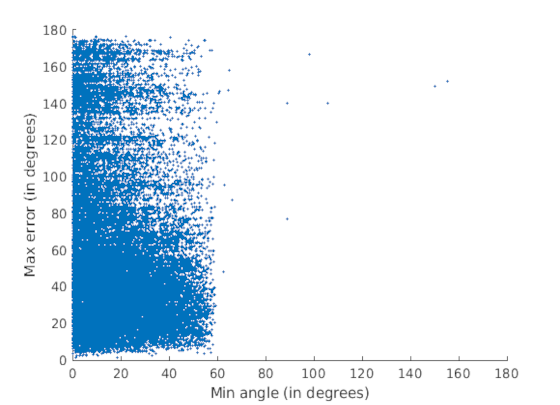
Tower of London |
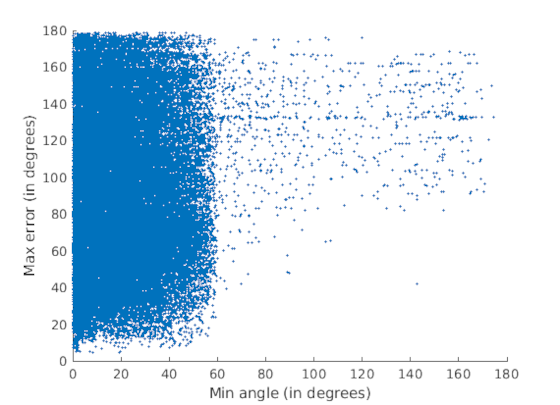
Union Square |
The scatter plots are displayed between minimum angle in triangles (x-axis) and maximum error in input directions in triangles (y-axis). These reveal that there is abundance of skewed triangles in the datasets. Moreover, there is no correlation between skewed triangles and presence of outliers. Removal of skewed triangles leads to improved translation accuracy, a higher number of 3D points triangulated and faster convergence of bundle adjustment.
Publication
-
Sensitivity in Translation Averaging (Lalit Manam and Venu Madhav Govindu), Neural Information Processing Systems, 2023. [bibtex]





