Lalit Manam, Venu Madhav Govindu
Translation averaging solves for 3D camera translations given many pairwise relative translation directions. The mismatch between inputs (directions) and output estimates (absolute translations) makes translation averaging a challenging problem, which is often addressed by comparing either directions or displacements using relaxed cost functions that are relatively easy to optimize. However, the distinctly different nature of the cost functions leads to varied behaviour under different baselines and noise conditions. In this paper, we argue that translation averaging can benefit from a fusion of the two approaches. Specifically, we recursively fuse the individual updates suggested by direction and displacement-based methods using their uncertainties. The uncertainty of each estimate is modelled by the inverse of the Hessian of the corresponding optimization problem. As a result, our method utilizes the advantages of both methods in a principled manner. The superiority of our translation averaging scheme is demonstrated via the improved accuracies of camera translations on benchmark datasets compared to the state-of-the-art methods.
| |
|
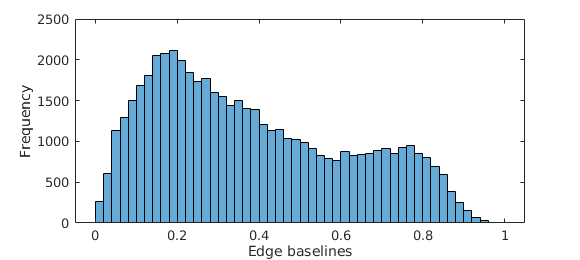
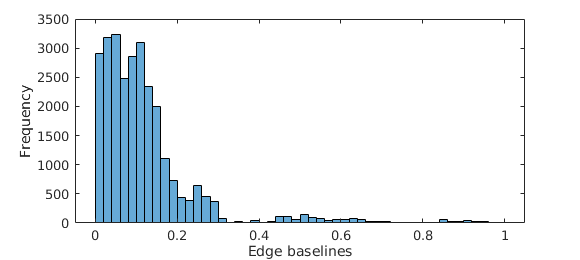
| Montreal Notre Dame |
Yorkminster |
Figure 1. Histograms of normalized ground truth baselines.
| |
|
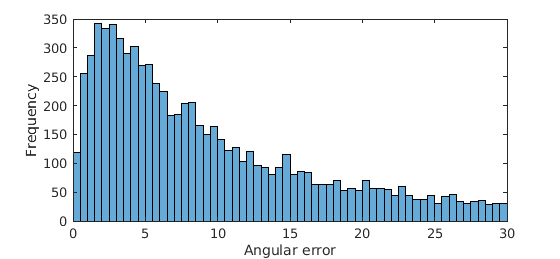
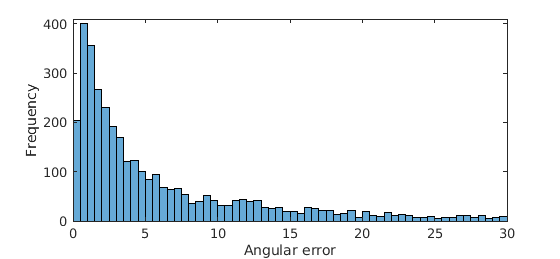
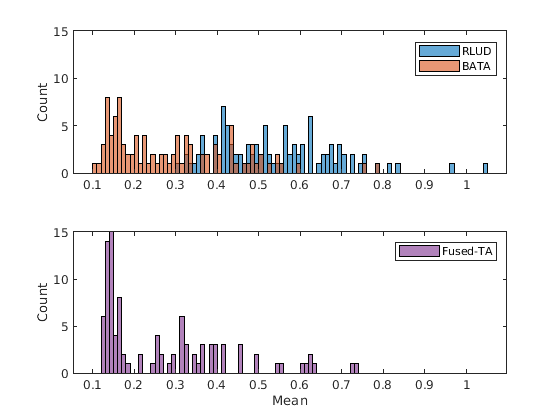
| Ellis Island |
Madrid Metropolis |
Figure 2. Histograms of input direction errors (in degrees).
Results
Synthetic Data
| |
|
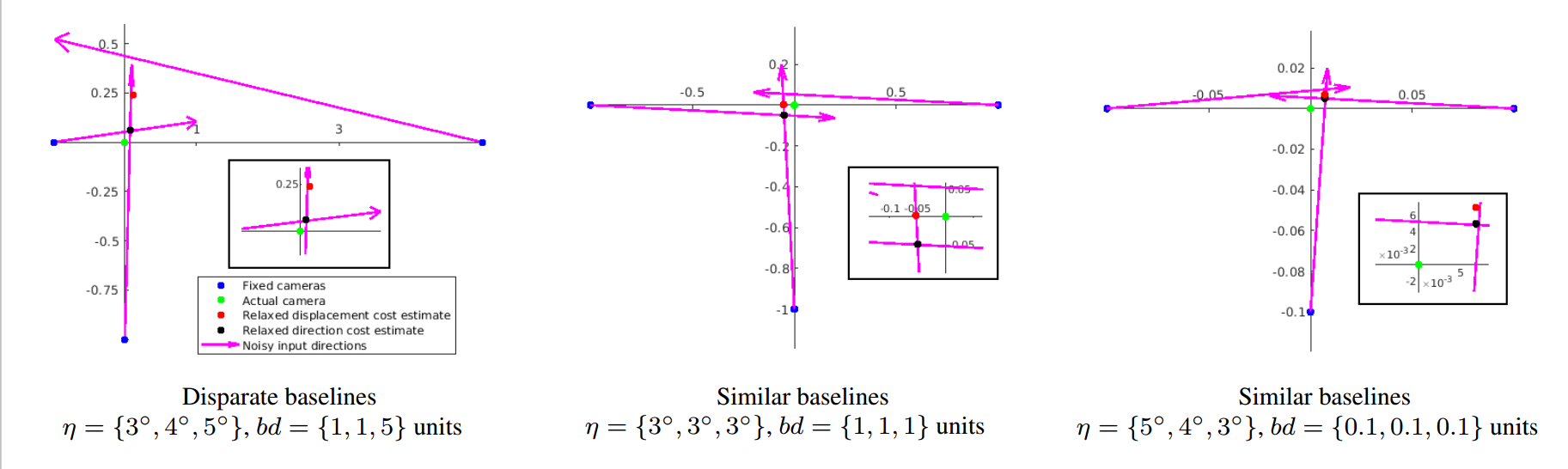
| Disparate baselines with input noise \( \sigma = 5\) |
Similar baselines with input noise \( \sigma = 5\) |
Figure 3. Histogram of mean errors for synthetic datasets on noisy data with different baselines. The leftward shift indicates the superior performance of our method.
Real Data
| Dataset |
1DSfM |
LUD |
ShapeFit |
BATA |
Fused-TA (Ours) |
| Alamo |
2.4 |
3.0 |
2.6 |
2.4 |
2.4 |
| Ellis Island |
32.3 |
26.0 |
15.6 |
25.3 |
17.5 |
| Montreal Notre Dame |
1.9 |
2.4 |
2.3 |
1.9 |
1.8 |
| NYC Library |
3.1 |
3.0 |
3.6 |
2.5 |
2.3 |
| Piazza del Popolo |
7.2 |
5.5 |
15.8 |
5.0 |
4.5 |
| Piccadilly |
2.2 |
2.6 |
2.4 |
2.3 |
2.1 |
| Roman Forum |
4.3 |
8.6 |
8.6 |
4.4 |
5.3 |
| Tower of London |
8.0 |
10.7 |
8.6 |
6.9 |
6.2 |
| Trafalgar |
11.7 |
7.6 |
8.3 |
6.9 |
6.5 |
| Union Square |
9.2 |
8.5 |
14.3 |
8.1 |
7.9 |
| Vienna Cathedral |
12.8 |
6.5 |
7.1 |
6.5 |
6.1 |
Table 1. Median camera translation errors (in meters) on 1DSfM datasets.
Publication
- Fusing Directions and Displacements in Translation Averaging , International Conference on 3D Vision, 2024 (Oral Presentation). [bibtex]