Adaptive Annealing for Robust Geometric Estimation

Chitturi Sidhartha, Lalit Manam, Venu Madhav Govindu
[Paper] [Supp] [Poster] [Video] [Code] (Updated July 27, 2023)

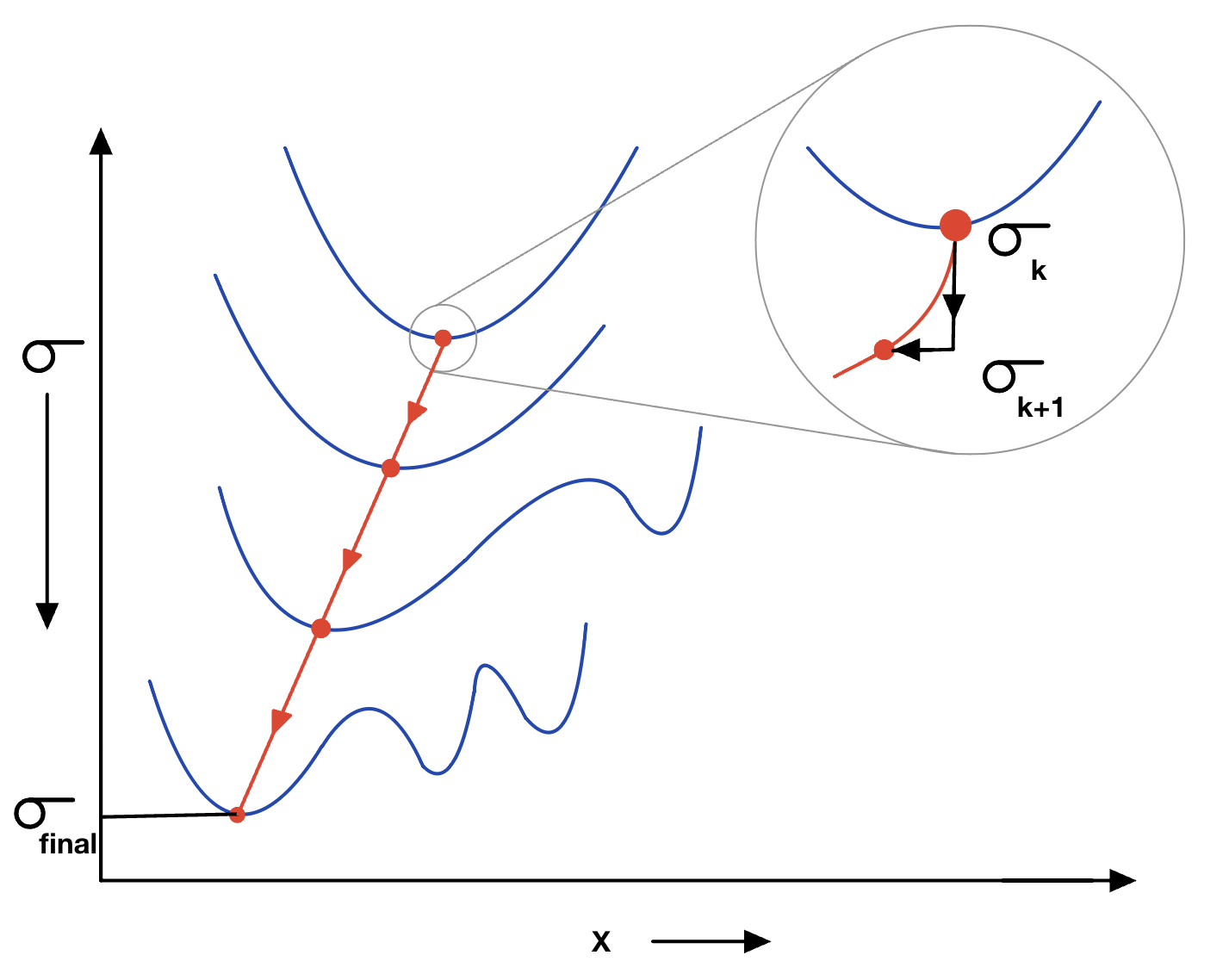
Pipeline

Geometric estimation problems in vision are often solved via minimization of statistical loss functions which account for the presence of outliers in the observations. The corresponding energy landscape often has many local minima. Many approaches attempt to avoid local minima by annealing the scale parameter of loss functions using methods such as graduated non-convexity (GNC). However, little attention has been paid to the annealing schedule, which is often carried out in a fixed manner, resulting in a poor speed-accuracy trade-off and unreliable convergence to the global minimum. In this paper, we propose a principled approach for adaptively annealing the scale for GNC by tracking the positive-definiteness (i.e. local convexity) of the Hessian of the cost function. We illustrate our approach using the classic problem of registering 3D correspondences in the presence of noise and outliers. We also develop approximations to the Hessian that significantly speeds up our method. The effectiveness of our approach is validated by comparing its performance with state-of-the-art 3D registration approaches on a number of synthetic and real datasets. Our approach is accurate and efficient and converges to the global solution more reliably than the state-of-the-art methods.

Overview

Pipeline

Figure 1. Flowchart of GNC procedure

The figure shows the general Graduated NonConvexity (GNC) procedure. Generally, \( \gamma_k \) is fixed. Small values of fixed \( \gamma_k \) gives higher accuracy but at the cost of increased annealing stages, while for small fixed \( \gamma_k \), the number of stages decrease but with reduced accuracy. Our annealing scheme balances the two by choosing \( \gamma_k \) adaptively. The observations are summarized below.
GNC Strategy # of stages in GNC Accuracy
Small \( \gamma \) (fixed) \(\boldsymbol{\uparrow}\) \(\boldsymbol{\uparrow}\)
Large \( \gamma \) (fixed) \(\boldsymbol{\downarrow}\) \(\boldsymbol{\downarrow}\)
Adaptive \( \gamma \) [Ours] \(\boldsymbol{\downarrow}\) \(\boldsymbol{\uparrow}\)
Desirable \(\boldsymbol{\downarrow}\) \(\boldsymbol{\uparrow}\)

Table 1. Impact of different annealing schemes

Method

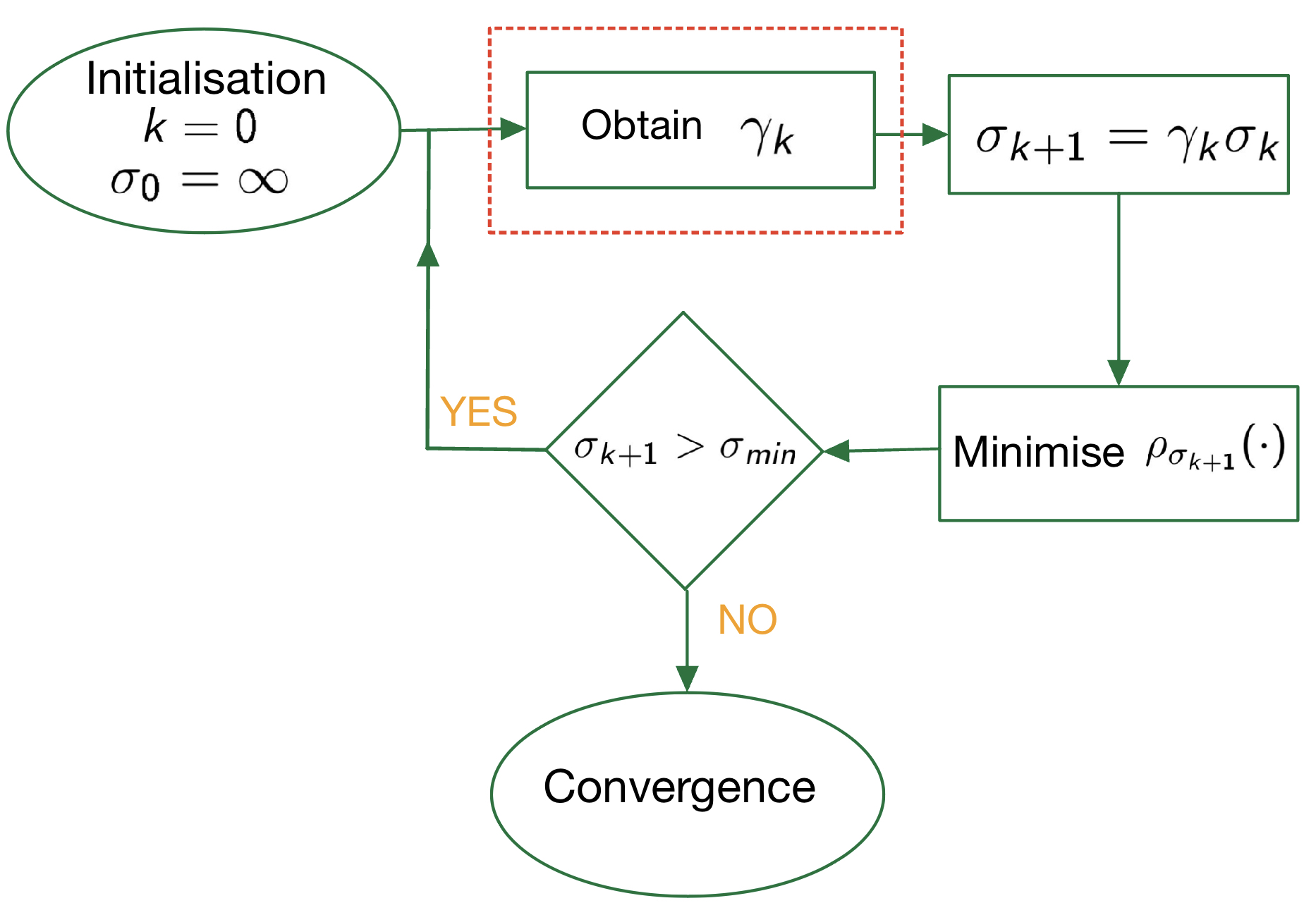
The steps can be summarized as follows:
  • Given the current solution \(x_k^*\), choose \(\sigma_{k+1}\) as: \begin{align*} {\sigma_{k+1} = \underset{\sigma\leq \sigma_{k}}{\operatorname{min}} \left\lbrace\sigma | \lambda_{min}\left(\mathbf{H}_{\mathbf{x}_k^*} \left(\sigma\right)\right)>\lambda_{T} >0 \right\rbrace} \end{align*}
  • The least squares cost's gradient \(\mathbf{g}_{LSQ}\) and Hessian \(\mathbf{H}_{LSQ}\) is given as: \begin{gather} \mathbf{H} (\sigma) = \sum_{i}^{n} \left(-l_i \frac{\mathbf{g}_{LSQ,i} \mathbf{g}_{LSQ,i}^T}{\|r_i\|^2} + m_i \mathbf{H}_{LSQ,i}\right), \label{exp:robustHessian}\\ \text{ where } l_i = \frac{\rho'(\|{\mathbf{r}_i}\|)}{\|\mathbf{r}_i\|}-\rho''(\|\mathbf{r}_i\|) and m_i = \frac{\rho'(\|\mathbf{r}_i)\|}{\|\mathbf{r}_i\|} \end{gather}
  • \(\lambda_{min}(\mathbf{H}_{\mathbf{x}_k^*}(\sigma))\) is monotonic in \(\sigma \Rightarrow\) binary search is used to find \(\sigma_{k+1}\)
  • Approximate \(l_i\)'s and \(m_i\)'s used to make the Hessian (\(\mathbf{H}\)) amenable for cheap evaluations of \(\lambda_{min}(\mathbf{H})\).

    • Illustration on Pairwise 3D Registration

    Given correspondences \(\left\lbrace \mathbf{a}_i, \mathbf{b}_i \right\rbrace\) between two unaligned 3D scans, find the transformation \(\mathbf{R},\mathbf{t}\) that aligns the scans. \begin{align*} \quad \min_{\left(\mathbf{R},\mathbf{t}\right)} \sum_{i=1}^{N} \rho_{\sigma}(\|\mathbf{a}_i -\mathbf{R} \mathbf{b}_i-\mathbf{t} \|) \end{align*}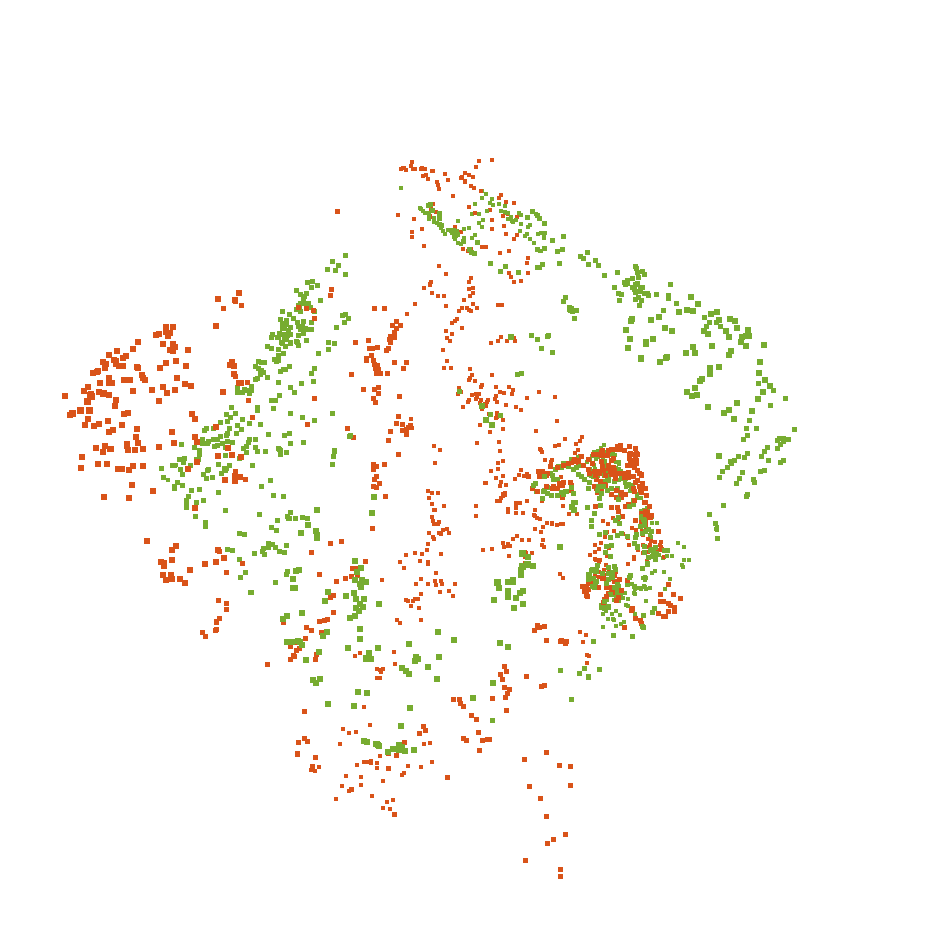
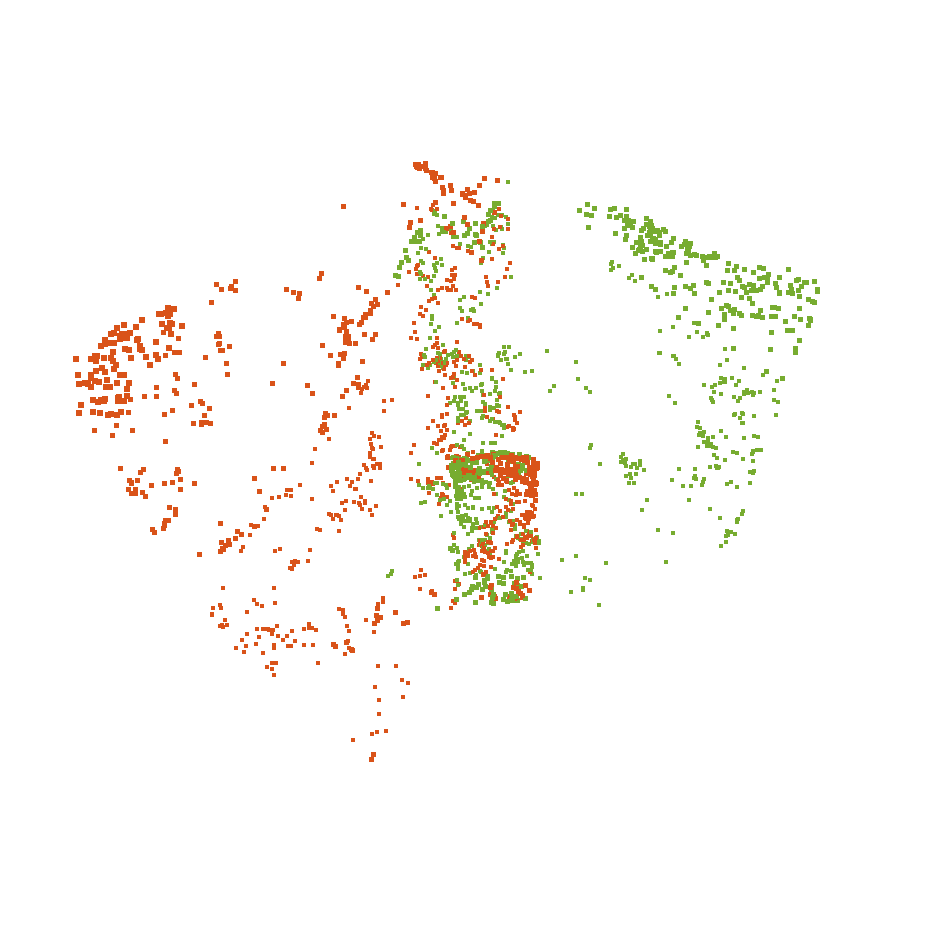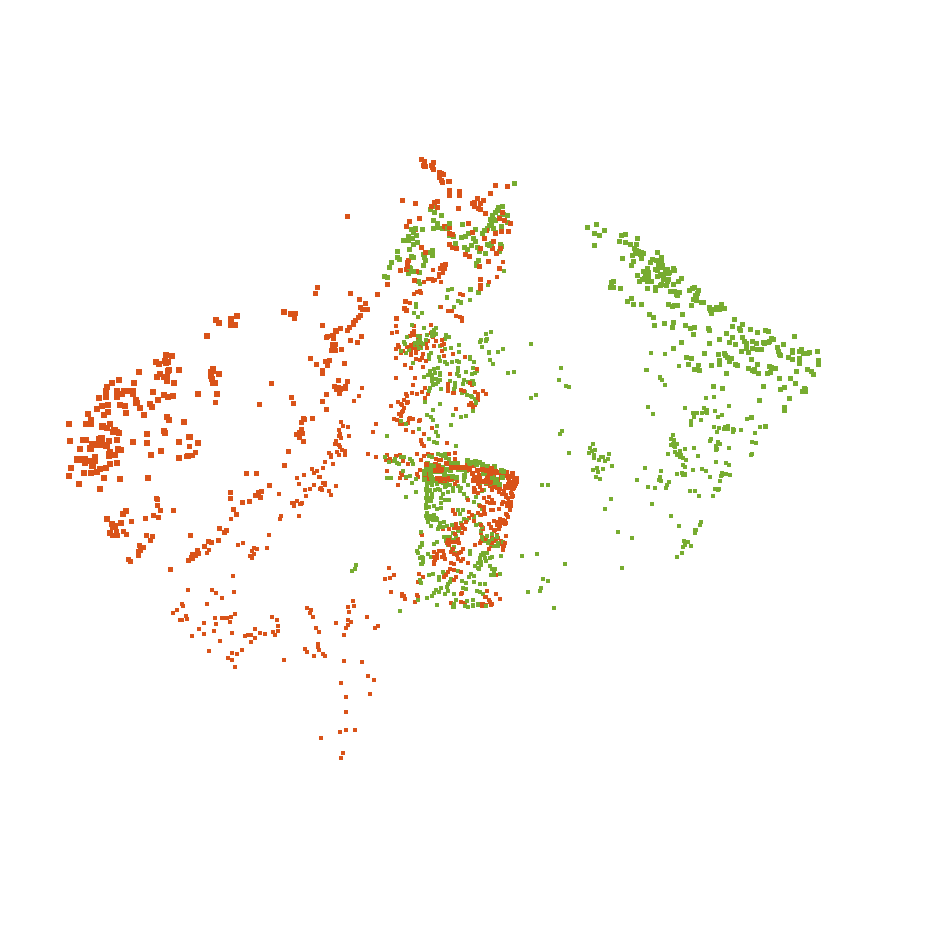    SE3Reg Teaser++ GNCp Ground Truth
    SE3Reg Teaser++ GNCp (Ours) Ground Truth

    Figure 2. Two point clouds (red and green) with a low overlap in the MIT Lab sequence of 3D Match dataset

    Publication

    1. Adaptive Annealing for Robust Geometric Estimation (Chitturi Sidhartha, Lalit Manam and Venu Madhav Govindu), IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2023. [bibtex]